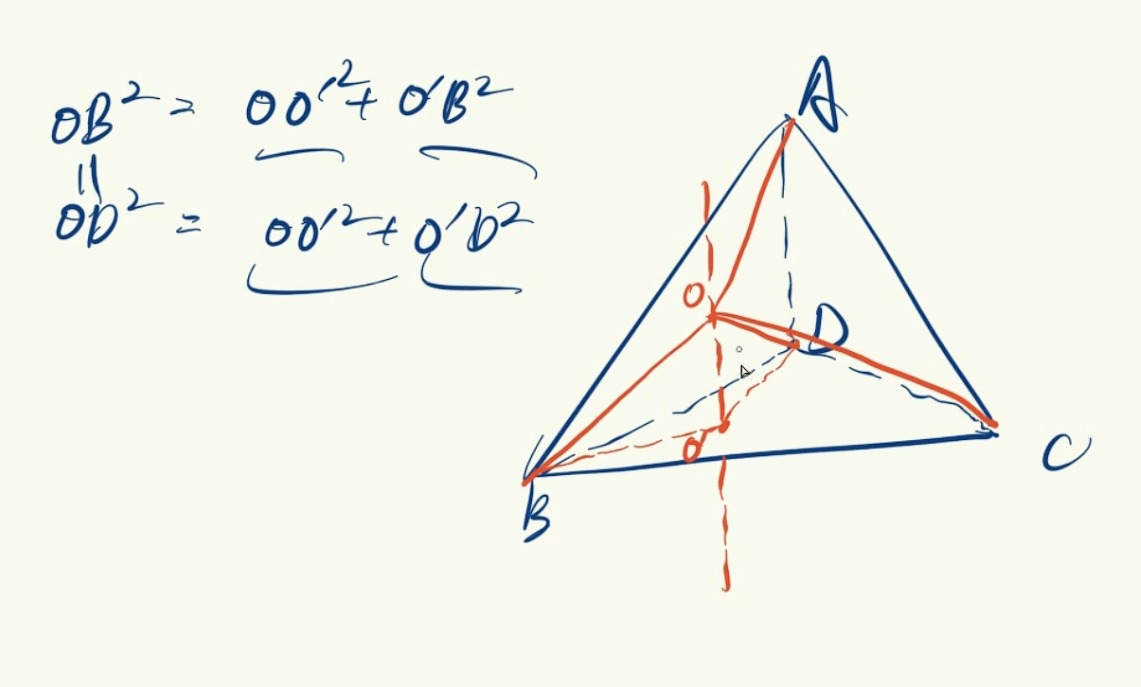数学外接球最基础笔记1
1、墙角模型
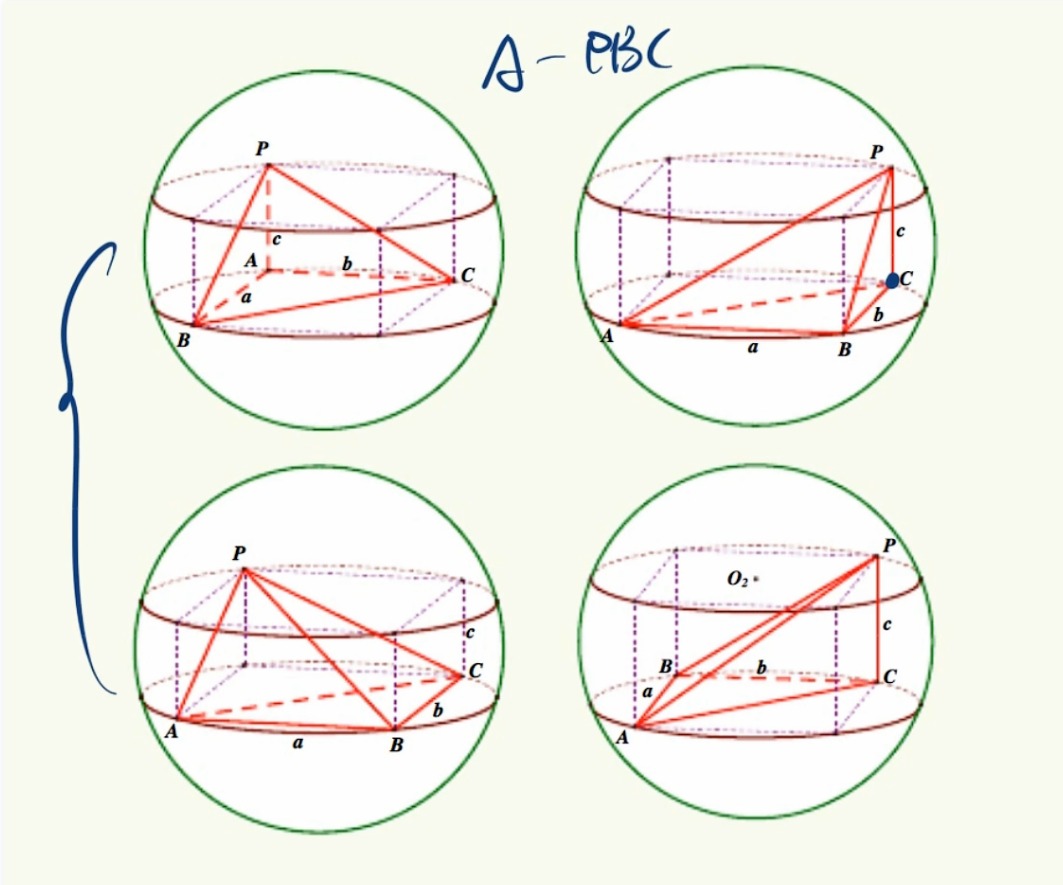
若遇到墙角模型,直接构建长方体,以三条相互垂直的线段为棱即可(根据垂直关系去补)
之后求长方体的体对角线即为外接球直径
墙角模型可以进行推广,比如底面为直角三角形,一条棱在与之垂直的平面上。
常见变形
利用三垂线定理证SB垂直于AC
之后证明出三条侧棱两两垂直,以S为墙角(顶点)构建长方体
注意:若遇到棱垂直于面,可考虑构造圆柱,或按照圆柱外接球公式、正弦定理及余弦定理求解
2、外心法
三棱锥
做底面的外心(中垂线交点)
过外心做一条直线垂直于该底面,则直线上任一点到底面三点距离相等
令O点到顶点距离等于其到BCD的距离
常见 直角三角形外心为斜边中点
求外心时可能会用到
正弦定理(初中数学知识)
余弦定理 (搭配正弦定理算余弦,从而推出正弦)
3、对于特殊的外接球问题
换汤不换药,还是通过找外心,做垂直,列方程 算出球心位置以及球的半径
以下为ChatGPT给出的参考计算方案
一个几何体的外接球是能够完全包围该几何体的最小球,通常被称为最小外接球。对于一些常见的几何体,我们可以使用特定的公式来计算它们的外接球半径。
以下是一些常见几何体外接球半径的计算公式:
-
正方体:
对于一个边长为 (a) 的正方体,其外接球半径 (R) 可以通过以下公式计算:
[ R = \frac{a}{2} \sqrt{3} ] -
长方体:
对于一个长、宽、高分别为 (a)、(b) 和 (c) 的长方体,其外接球半径 (R) 可以通过以下公式计算:
[ R = \frac{\sqrt{a^2 + b^2 + c^2}}{2} ] -
球体:
对于一个半径为 (r) 的球体,其外接球半径与内接球半径相同,即 (R = r)。 -
三角形:
对于一个三角形,其外接圆半径 (R) 可以通过以下公式计算,其中 (a)、(b) 和 (c) 分别为三角形的三边长度:
[ R = \frac{abc}{4K} ]
其中 (K) 是三角形的面积,可以通过海伦公式(Heron’s Formula)计算:
[ K = \sqrt{s(s-a)(s-b)(s-c)} ]
其中 (s) 是半周长,即 (s = \frac{a+b+c}{2})。 -
四面体:
对于一个四面体,其外接球半径 (R) 可以通过以下公式计算,其中 (V) 是四面体的体积,而 (a), (b), (c), (d) 分别为四面体的四个面上的三角形的面积:
[ R = \frac{\sqrt{(abc + abd + acd + bcd)^2 - 2(abc)^2 - 2(abd)^2 - 2(acd)^2 - 2(bcd)^2}}{12V} ]
请注意,以上公式假定几何体的形状是理想的,并且不受变形。在实际应用中,可能需要考虑形状变化引起的影响。